sandbox/Antoonvh/coalescence.c

    Coalescence may happen when droplet’s interfaces are close. Image via Prof. Schroen (WUR)

    When Coalescence is the Essence

    Two droplets are launched towards each other. This example shows how different set ups can lead to coalcesence or not.

    //#include "grid/multigrid.h"
#include "navier-stokes/centered.h"
#include "vof.h"
#include "tension.h"
#include "view.h"

    There are in total 4 droplets in two binary collisions,

    scalar f1[], f2[], f3[], f4[], * interfaces = {f1, f2, f3, f4};

    A criterium for coalescence

    Since I am not burdened with the knowledge of how coalescence actually works, I can freely guess a rule for this subgrid-scale microscopic process. Here the rule is: Coalescence occurs when the distance between the (2D) interfaces is at maximum some critial distance (CD) over atleast some critical length (CL). The function below checks if this is the case for two vof fiels s1 and s2.

    double CD = 5E-4;
double CL = 0.1;
bool coalcheck(scalar s1, scalar s2){
  face vector s;
  double length = 0;
  foreach(){
    if (s1[] > 0.1 && s1[] < 0.9 && s2[] > 0.1 && s2[] < 0.9){
      coord n1 = facet_normal (point, s1, s);
      coord n2 = facet_normal (point, s2, s);
      double alpha1 = plane_alpha (s1[], n1);
      double alpha2 = plane_alpha (s2[], n2);
      coord segment1[2];
      coord segment2[2];
      int nd = 0;
      if (facets (n1, alpha1, segment1) == 2 && facets (n2, alpha2, segment2) == 2){
	double dist = HUGE;
	for (int m = 0; m < 2; m++){
	  for (int mm = 0; mm < 2; mm++){
	    dist = sq(segment1[m].x - segment2[mm].x) + sq(segment1[m].y - segment2[mm].y);
	    if (dist < sq(CD/Delta))
	      nd++;
	    if (nd == 2)
	      length += pow(sq(segment1[0].x - segment1[1].x) +
			    sq(segment1[0].y - segment1[1].y), 0.5)*Delta;
 	  }
	}
      }
    }
  }
  if (length > CL)
    return true;
  return false;
}

    Vof fields s1 and s2 can be coalesced with the function below. Noting that we still rely on numerical coalescence to merge the fluids.

    void coal(scalar s1, scalar s2){
  foreach()
      s1[] += min(s2[], 1.);
    scalar * scr = {NULL}; //Scratch
    for (scalar s in interfaces){
      if (s.i != s2.i)
	scr = list_add(scr, s);
    }
    interfaces = scr;
    delete({s2});  //We cannot free({s2}) from the heap
}

    The set-up follows the non-coalescence example of Stephane.

    int main(){
  foreach_dimension()
    periodic(left);
  N = 256;
  size (4.);
  origin (-L0/2., -L0/2.);
  const face vector muc[] = {0.01, 0.01};
  mu = muc;
  f1.sigma = f2.sigma = f3.sigma = f4.sigma = 1.;
  run();
}

    It is of pivotal importance to orient the interfaces properly.

    event init (t = 0){
  fraction (f1, - (sq(x + 1.) + sq(y + 1) - sq(0.4)));
  fraction (f2, - (sq(x - 1.) + sq(y + 1) - sq(0.5)));
  fraction (f3, - (sq(x - 0.8) + sq(y - 1.01) - sq(0.3)));
  fraction (f4, - (sq(x + 0.6) + sq(y - 0.99) - sq(0.3)));
  foreach()
    u.x[] = f4[] + f1[] - f2[] - f3[];
}

    Each time step we check if interfaces coalesce. We actually dubble check this, for no good reason. Noting that 1% of the time is spent in this event.

    event check_for_coal(i++){
  int j = 0;
  for (scalar s1 in interfaces){
    for (scalar s2 in interfaces){
      if (s1.i != s2.i){
	if (coalcheck(s1, s2)){
	  coal(s1, s2);
	  j = 1; // A single coalescence event per time step has to suffice
	}
      }
      if (j == 1)
	break;
    }
    if (j == 1)
      break;
  }
}

    A movie of the fluids is generated.

    event movie (t += 0.025; t <= 10.){
  clear();
  double cc = 1;
  for (scalar s in interfaces){
    scalar b[];
    foreach()
      b[] = s[] > 0.5? s[] : nodata;
    squares("b",min = 0, max = cc);
    draw_vof (s.name, lw = 3);
    cc += 1.;
  }
  box();
  save ("movie.mp4");
}

#if TREE
event adapt(i++)
  adapt_wavelet(interfaces, (double[]){0.001, 0.001, 0.001, 0.001}, 8, 4);
#endif

    Result

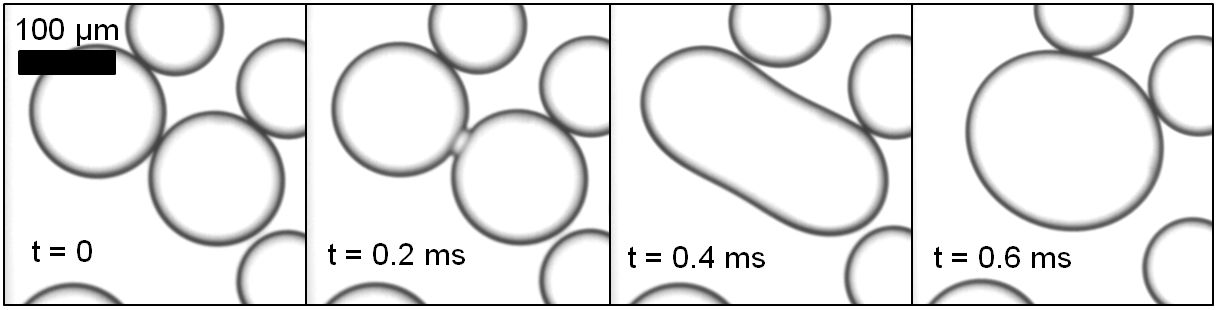
    The criteria for coalescence were hand-tuned to achieve the following result:

    The bigger drops coalesce, wheareas the smaller ones do not