mandelbrot3.c

The Mandelbrot set

The Mandelbrot set

The Mandelbrot set is vizualized and studied using a quadtree.

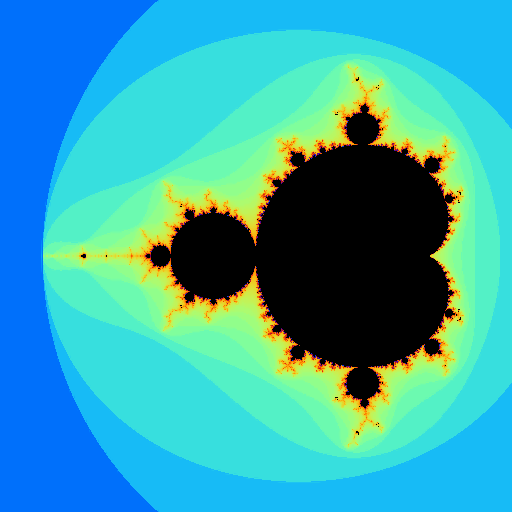
The result:
drawing

#include "utils.h"

A function is formulated that returns the number of iterations it takes until \|c_n|\ > 2 with n_{\mathrm{max}} = 1000 and a MACRO is defined that computes the corresponding color code.

double Nmax = 1000;
trace
int N_iters (double xp, double yp) {
  int j = 0;
  double a = xp;
  double b = yp;
  double c; //scratch
  while (sq(a) + sq(b) < 4 && j++ <= Nmax) {
    c = (a*a) - (b*b) + xp;// Real part 
    b = (2.*a*b) + yp; //Imag part
    a = c;
  }
  return j;
}
#define COLOR_CODE (log(N_iters (x, y) + 1.))

Newly refined points should obtain the proper color code. Since the computations start from a coarse grid, the coarse-level values will already be computed when they are needed.

static inline void refine_mandel (Point point, scalar s) {
  foreach_child() 
    s[] = COLOR_CODE;
}

static inline void its_already_there (Point point, scalar s) {;}

void rainbow (double cmap[NCMAP][3]);

scalar m[];
int main() {
  m.refine = refine_mandel;
  m.restriction = its_already_there;

The domain is defined, the grid is initialized and the first color codes are computed.

  L0 = 3.;
  X0 = -2.25;
  Y0 = -L0/2.;
  init_grid (2);
  for (int l = depth() - 1; l <= depth(); l++) 
    foreach_level(l)
      m[] = COLOR_CODE;

We refine the grid where it’s needed until the maximum resolution is achieved. For each doubling of the resolution the number of the used points is counted.

  int max_lev = 14;
  for (int lev = depth() + 1 ; lev <= max_lev; lev++) {
    while (adapt_wavelet ({m}, (double[]){log(Nmax + 1.)/NCMAP}, lev).nf);
    printf("%d\t%ld\n", depth(), grid->n);

At a resolution of 512 \times 512 we output an image, masking the set itself. The used points are outputted to a file.

    if (depth() == 9) {
      scalar msk[];
      foreach()
	if (m[] > log(Nmax + 0.9))
	  msk[] = -1;
      output_ppm (m, file = "mandel_ad.png", map = rainbow,
		  min = 0, max = log (Nmax + 1.), mask = msk,
		  n = 1 << depth(), linear = true);
      FILE * fp = fopen ("points", "w");
      foreach()
	fprintf (fp, "%g\t%g\t%d\n", x ,y, level); 
    }
  }
}

void rainbow (double cmap[NCMAP][3]) {
  for (int i = 0; i < NCMAP - 1; i++) {
    cmap[i][0] = sq(sin((double)i*M_PI/130.));
    cmap[i][1] = sq(sin(((double)i + 30.)*M_PI/130.));
    cmap[i][2] = sq(sin(((double)i + 60.)*M_PI/130.));           
  }
  for (int i = 0; i < 3; i++)
    cmap[NCMAP - 1][i] = 0;
}