sandbox/Antoonvh/ti2.c
A proof of concept for the implicit-integral-equation solver
We look for the field S, defined as the line integral of s along the vector \mathbf{n};
\displaystyle S(\mathbf{x_0}) = \int_{\mathbf{x_0}} s\mathrm{d}\mathbf{n}
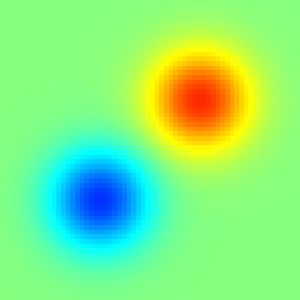
The field to integrate (s)
The code solves for S, by solving the implicit equation,
\displaystyle \mathbf{n}\cdot\left(\nabla \left(\mathbf{n}\cdot\nabla S\right)\right) = -\mathbf{n}\cdot \nabla s,
in many directions:
Looks good for all angles
set polar
set grid polar
unset xtics
unset ytics
set xlabel 'MG cycles'
set border 0
set style fill solid 0.5
set rrange [0.1 : 35]
set size square
set key right outside
plot 'out' u 1:2 with filledcurve above r = 20 notitle , 'out' u 1:2 w l lw 2 t 'MG cycles' ,\
'out' u 1:3 with filledcurve above r = 10 notitle , 'out' u 1:3 w l lw 2 t 'Relaxation sweeps'Convergence history as a function of the angle (script)
The convergence for the near-grid-alliged integrations is poor.
#include "integrator2.h"
#include "utils.h"
int main() {
L0 = 6;
X0 = Y0 = Z0 = -L0/2;
init_grid (N);
scalar s[], S[];
foreach()
s[] = exp(-sq(x - 1) - sq(y - 1) - sq(z))
- exp(-sq(x + 1) - sq(y + 1) - sq(z));
boundary ({s});
output_ppm (s, file = "source.png", n = 300);
for (double angle = 0; angle <= 2*pi + 1e-5; angle += pi/50) {
coord n = (coord){cos(angle)- 0.01, sin(angle) + 0.01, 0};
mgstats lint = integrate_dn (S, s, n);
printf ("%g %d %d\n", angle, lint.i, lint.nrelax);;
output_ppm (S, file = "S.mp4", n = 300, min = -sqrt(pi), max = sqrt(pi));
}
}