reinit_LS.c

LS_reinit() test case
- References

LS_reinit() test case

Note that a maintained version of this test case is /src/test/redistance-ellipse.c.

// still a bug with the extract_root_x => divergence.

This case is extracted from Russo et al.,1999 we initialize a perturbed distance field, where the zero level-set is an ellipse of the form: \displaystyle \phi (x,y,0) = f(x,y) \times g(x,y) where the perturbation is : \displaystyle f(x,y) = \epsilon + (x - x_0)^2 +(y - y_0)^2 and the ellipse is : \displaystyle g(x,y) = \left( \sqrt{\frac{x^2}{A^2}+\frac{y^2}{B^2}} -R \right) with A=2, B=1, R = 1 , x_0 = 3.5, y_0 = 2..

We want to recover a perfect distance field, remove the initial perturbation.

#define BICUBIC 1
#define BGHOSTS 2

popinet/distance_point_ellipse.h: No such file or directory

#include "popinet/distance_point_ellipse.h"
#include "alimare/alex_functions.h"
#include "alimare/LS_reinit.h"
#include "alimare/basic_geom.h"
#include "view.h"

double perturb (double x, double y, double eps, coord center){
  return eps + sq(x - center.x) + sq(y - center.y);
}

void draw_isolines(scalar s, double smin, double smax, int niso, int w){
  vertex scalar vdist[];
  cell2node(s,vdist);
  
  boundary ({vdist});
  for (double sval = smin ; sval <= smax; sval += (smax-smin)/niso){
    isoline ("vdist", sval, lw = w);
  }
}

#define Pi 3.141592653589793

norm mynorm(scalar f, scalar f2, double threshold){

For this test case, we use a special norm defined by the author, which ignores the points below a specific threshold, f > \text{threshold}

  double avg = 0., rms = 0., max = 0., volume = 0.;
  foreach(reduction(max:max) reduction(+:avg) 
    reduction(+:rms) reduction(+:volume)) 
    if (f[] != nodata && dv() > 0. && f2[] > threshold) {
      double v = fabs(f[]);
      if (v > max) max = v;
      volume += dv();
      avg    += dv()*v;
      rms    += dv()*sq(v);
    }
  norm n;
  n.avg = volume ? avg/volume : 0.;
  n.rms = volume ? sqrt(rms/volume) : 0.;
  n.max = max;
  n.volume = volume;
  return n;
}

norm mynorm2(scalar f, scalar f2, double threshold){

This second norm selects points such that |f| < \text{threshold}.

  double avg = 0., rms = 0., max = 0., volume = 0.;
  foreach(reduction(max:max) reduction(+:avg) 
    reduction(+:rms) reduction(+:volume)) 
    if (f[] != nodata && dv() > 0. && fabs(f2[]) < threshold) {
      double v = fabs(f[]);
      if (v > max) max = v;
      volume += dv();
      avg    += dv()*v;
      rms    += dv()*sq(v);
    }
  norm n;
  n.avg = volume ? avg/volume : 0.;
  n.rms = volume ? sqrt(rms/volume) : 0.;
  n.max = max;
  n.volume = volume;
  return n;
}



scalar dist[];
scalar * level_set = {dist};

int main() {

  origin (-5., -5.);
  L0 = 10;

  int MAXLEVEL = 6;
  for(MAXLEVEL = 6; MAXLEVEL < 9; MAXLEVEL++){
    init_grid (1 << MAXLEVEL);  
  
    double A = 4., B=2.;
    coord  center_perturb = {3.5,2.};
    foreach(){
      double a,b;
      // dist[] = DistancePointEllipse(A,B,x,y,&a, &b);
      dist[] = DistancePointEllipse(A,B,x,y,&a, &b)*
      perturb(x,y, 0.1, center_perturb);
    }
    boundary({dist});
  
    squares ("dist", map = cool_warm, min = -2, max = 2);
    draw_isolines(dist, -2., 2., 20, 1);
    save("dist_init.png");

    int nbit = LS_reinit(dist, it_max = 1 << (MAXLEVEL+1));
    squares ("dist", map = cool_warm, min = -2, max = 2);
    draw_isolines(dist, -2., 2., 20, 1);
    save("dist_first_reinit.png");

    
    scalar err[],LogErr[];
    foreach(){
      double a,b;
      err[] = dist[] - DistancePointEllipse(A,B,x,y,&a, &b);
      LogErr[] = log(fabs(err[])+1.e-16);
    }
    boundary({err,LogErr});
    norm n = mynorm(err,dist,-0.8);
    norm n2 = mynorm2(err,dist,1.2*L0/(1 << grid->maxdepth));
    fprintf(stderr, "%d %g %g %g %g %g %g %d\n",1<<MAXLEVEL, n.avg, n.rms,n.max,
      n2.avg, n2.rms,n2.max, nbit);


    if(MAXLEVEL == 8){
      squares ("LogErr", min = log(n.max)-6, max = log(n.max));
      save("err.png");
    }
  }
  exit(1);
}

We show here the initial and final level-set for the same isovalues.

Initial level-set

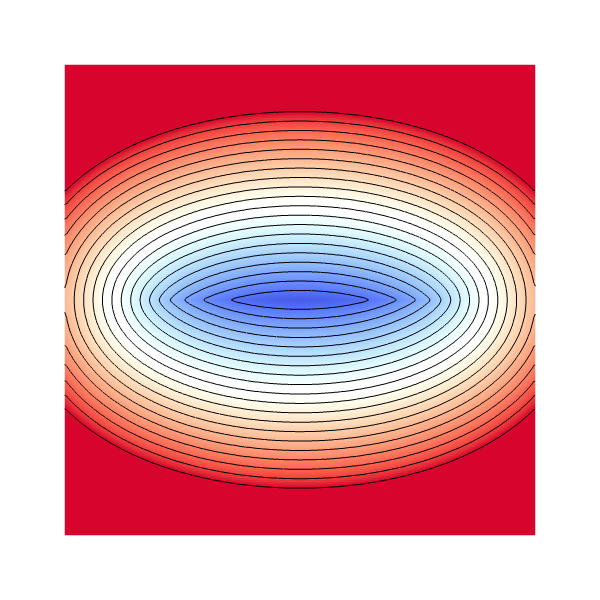
First reinit

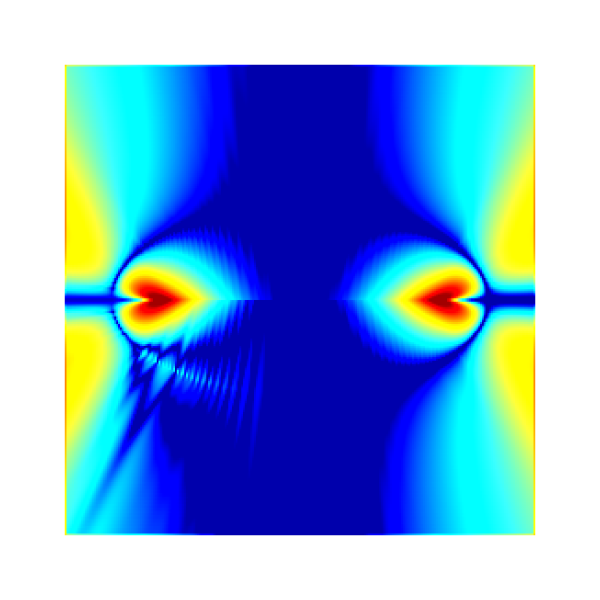
$Error, logscale between 10^{-4} and 10^{-1}$

Error, logscale between 10^{-4} and 10^{-1}

f(x) = a + b*x
f1(x) = a1 + b1*x
f2(x) = a2 + b2*x
fit f(x) 'log' u (log($1)):(log($2)) via a,b
fit f1(x) 'log' u (log($1)):(log($3)) via a1,b1
fit f2(x) 'log' u (log($1)):(log($4)) via a2,b2
ftitle(a,b) = sprintf("%.2f-%4.2f x", a, -b)
set logscale xy
set xrange [32:512]
set xtics 32,2,512
set format y "%.1e"
plot 'log' u 1:2 t 'avg', exp(f(log(x))) t ftitle(a,b), \
    'log' u 1:3 t 'rms', exp(f1(log(x))) t ftitle(a1,b1), \
    'log' u 1:4 t 'max', exp(f2(log(x))) t ftitle(a2,b2)

error analysis (script)

f(x) = a + b*x
f1(x) = a1 + b1*x
f2(x) = a2 + b2*x
unset logscale
unset xrange
fit f(x) 'log' u (log($1)):(log($5)) via a,b
fit f1(x) 'log' u (log($1)):(log($6)) via a1,b1
fit f2(x) 'log' u (log($1)):(log($7)) via a2,b2
ftitle(a,b) = sprintf("%.2f-%4.2f x", a, -b)
set logscale xy
set xrange [32:512]
set xtics 32,2,512
set format y "%.1e"
plot 'log' u 1:5 t 'avg', exp(f(log(x))) t ftitle(a,b), \
    'log' u 1:6 t 'rms', exp(f1(log(x))) t ftitle(a1,b1), \
    'log' u 1:7 t 'max', exp(f2(log(x))) t ftitle(a2,b2)

error analysis 0-level-set (script)

Here we study the value of the level-set function on a set of points where it is theoretically 0, we show that we have also a 3^{rd} convergence.

References

[russo_remark_2000]

Giovanni Russo and Peter Smereka. A remark on computing distance functions. Journal of Computational Physics, 163(1):51–67, 2000.